
Gravitational waves are “ripples in space time” that propagate through it like waves on water. That’s the common story and, for the most part, it’s right. But what does that mean? This is part four in my many-part series on general relativity. The first three parts introduce general relativity from the ground up. You can find them here:
- Galileo almost discovered general relativity
- General relativity is the dynamics of distance
- General relativity is the curvature of spacetime
Okay. Without further ado, gravitational waves!
Spooky Action at a Distance
First, I want to help you get an intuition for why gravitational waves should exist. So before we dive into the relativity, let’s step back for a moment and imagine boring old Newtonian gravity. Suppose we have a bowling ball (blue) and a marble (red), as shown in figure 2. We take the bowling ball and we move it periodically towards and away from the marble. As we do, we measure the strength of the gravitational pull the bowling ball exerts on the marble. It gets stronger as the bowling ball gets near and weaker as it moves further away. This is plotted in the bottom of figure 2.

Notice how wavy the gravitational strength looks? At this point, you might be tempted to call it a gravitational wave. But that temptation is leading you astray. See, an important property of waves is that they travel at finite speed. Information can’t travel instantly. But in Newtonian physics, the marble feels the change in the gravitational pull of the bowling ball instantly.
So what needs to change? Well, all we need to do is sprinkle a little bit of special relativity into the mix, since special relativity says that information can travel no faster than light. Then the wiggles plotted in figure 2 would be delayed. So the marble would only feel a gravitational force a bit after we move the bowling ball.
That would be a gravitational wave.
Since special relativity is basically true, and we feel gravitational forces, this should convince you that gravitational waves should exist. And it should also give you a sense on what a gravitational wave should be like. We should feel a temporary change in the “pull” from the gravity a distant object, which is an echo of its motion.
Gravitational Waves in General Relativity
But of course, gravitational waves don’t actually work the way I just described. Gravity is not a force, it’s a distortion in the way we measure distance. So how do gravitational waves work in this context? Well, in some sense, I already told you. Gravity is a distortion of how we measure distance. So a gravitational wave is a distortion in how we measure distance that travels.
Of course, there are some caveats, most of which I won’t get into. The most important caveat is how the distance distorts. Distances don’t just grow and shrink evenly in every direction. They grow in one direction and shrink in another. For example, if you took a circular ring of particles, I’m a fan of marbles, floating in outer space, and a gravitational wave passed by, you’d observe them distort into one ellipse and then another, as shown in figure 3. And this happens because the distances between the particles are changing. (For experts: I’m showing the + polarization. If you rotate by 45 degrees, you get the x polarization.)

Detecting Gravitational Waves, Part 1
So how would you detect a gravitational wave? Should we arrange a bunch of marbles in space and wait for them to distort? Well, in principle we could do that. But spacetime is very stiff and the distortion in distance from a gravitational wave is quite small, which is why we haven’t detected any gravitational waves yet. To see a distortion large enough that we could see, we’d need a very big ring of marbles.
Fortunately, we have one. An artist’s impression is shown in figure 4. Except our marbles are all neutron stars and our ring is millions of lightyears wide. Basically, each marble is a type of star called a millisecond pulsar, which is a neutron star that’s rotating very fast. For reasons I won’t get into, this makes it emit light (though usually not visible light) in a beam. And as it rotates, we see a pulse as the beam points towards us, like a lighthouse. To measure a distortion in spacetime due to a gravitational wave, we measure how long a pulse takes to reach us over many many pulses. If a pulse comes before or later than it should, that might be a gravitational wave! To see if it is, we need to check with all the pulsars in the “ring” to see if they distorted in the right way and do some fancy math.

This whole scheme is called pulsar timing, which is done with pulsar timing arrays. A pulsar timing array is a collaboration of people who use telescopes, like the one at Arecibo shown in figure 5, that keep track of millisecond pulsars and do statistics to see if they’ve detected a gravitational wave.

Detecting Gravitational Waves, Part 2
Pulsar timing is great and all… but is there a more… direct way we can find gravitational waves? Maybe something we can build on Earth? I’m glad you asked! We don’t really need a ring of particles, right? All we actually need are two very very precise rulers… set up so that we can measure distance growing in one direction and shrinking in another.
Fortunately, light makes an incredibly good ruler. So we can make our rulers out of laser light and compare them to detect a gravitational wave. That’s how the two LIGO detectors and detectors like them work. One of the detectors is shown in figure 6.

Each LIGO detector has two 4km long, vacuum-sealed, seismically isolated, supercooled laser arms that measure distance incredibly accurately. If you compare the distances measured in the two arms (which is actually all you can do because LIGO is a laser interferometer), the measurement in the difference is accurate to better than one part in ![]() . This means they can measure a change in distance one one-thousandth of the width of a proton.
. This means they can measure a change in distance one one-thousandth of the width of a proton.
The LIGO systems were recently upgraded and they’re coming online this year. So stay tuned in the following years for news of a gravitational wave detection!
Caveats
I should mention that moving a mass in a straight line back and forth, as in figure 2, is not enough to excite a gravitational wave in general relativity. The motion of the mass needs to have a so-called quadrupole moment. Most motions in the real world, such as orbiting a star, do have a quadrupole moment. But I wanted to mention this so that you’re not under the impression that all motion produces gravitational waves. Just most motion.
Stay Tuned!
I have a lot more to say about gravitational waves. But I think this is enough for now. In future posts, look forward to learning about the astrophysical systems that produce gravitational waves and listening to the sound of two black holes colliding.
Further Reading
I didn’t pull my description from a single source, this time. I used a bunch of textbooks, such as Spacetime and Geometry by Sean Carroll and Introduction to 3+1 Numerical Relativity by Miguel Alcubierre. But here’s some more accessible resources:
- My collaborators, the Simulating Extreme Spacetimes Collaboration, have a great article on gravitational waves.
- NANOGrav’s science page isn’t bad either.
- And here’s a nice blog post on gravitational waves and pulsar timing.
Related Reading
If you liked this post (and my other general relativity posts) you may be interested in some of my posts on relativistic astrophysics:

Thanks for sharing Jonah! Very interesting article. I look forward to your next one.
Thanks, Stan! I’m glad you liked it!
What are the Ligo detectors detecting? Would they be detecting that the Earth is passing through a gravitational wave?
That’s exactly right! When the earth passes through a gravitational wave (or a gravitational wave passes through the Earth), one arm of the LIGO detector will shrink and one arm will grow and we can detect that.
Why do you say that the motion of a mass on a straight back and forth line doesn’t have a quadrupole moment?
Possibly because I made a mistake. My thinking was that the quadrupole moment is
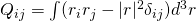
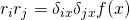
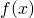 . Then the integrand always cancels because we have
. Then the integrand always cancels because we have
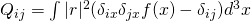
but since the mass is on a line,
for some function
But I see that doesn’t quite cancel. I’ll fix it. Thanks for the correction.
Oh wait, I don’t say that mass on a straight line doesn’t have a quadrupole moment, do I? I just say you need one.
Would it be fair to say that gravitational waves are produced by an accelerating mass, not unlike electromagnetic waves being produced by accelerating charged particles?
Yes it would! In particular, electromagnetic waves are caused by a changing “dipole moment” whereas gravitational waves are caused by a changing “quadrupole moment.”
If i have understood this, a gravitational wave is a stretch of space in one direction and a compression in the other perpendicular direction. But if space is stretched or compressed so is our measurement ruler.I guess it’s like the expansion of the universe light gets redshifted because it is stretched by the expansion.how can the ligo work to sense this stretch since the laser light must also be streched and compressed leading to a null result ? e
Great question! There are two answers to that. One is easy to understand, but a little wrong and one is harder to understand but correct. I’ll give you both.
HERE’S THE EASY ANSWER
One ruler that gets stretched and the other contracted. So the lengths of the rulers, RELATIVE TO EACH OTHER change, even if each ruler doesn’t measure any change in its own length.
HERE’S THE HARD ANSWER
RIght. The ruler analogy is actually hand-wavy. The “correct” way to think about it is to realize that the lasers in LIGO bounce between two mirrors, each of which is hanging from the ceiling. When the gravitational wave passes by, it distorts the distance between the two mirrors and the mirrors “perceive” this as motion relative to each other. This changes the way the laser behaves. And this is measurable (at least in principle) even if LIGO only had one arm.
But having two arms helps a huge amount. It doubles the strength of the signal and cancels out most of the laser noise. In practice, you need both arms.
Does this help?
Thanks for your explanation. I can’t help feeling that these two explanations are somewhat contradictory. if you only really need one arm of the interferometer then you cannot invoke a relative change between the two arms as the measurement process.
So if we just consider one arm, what is going on ? And how is a phase shift created by the gravitational wave? If we imagine that the distance to the mirrors is an exact number of wavelengths of the laser light, since the laser light is also affected by the gravitational wave in the same way, it will still have the exact number of wavelengths when the wave passes so there will be no observable phase shift ? Of course I am only considering the space changing part of the wave. Is there a time changing part as well ?
I have got another problem, and that is with coelescing Black Holes. Now I understood that as one approaches a black hole, time passes more slowly relative to normal time due to the gravitational potential. As an object falls into a black hole, as viewed from a distance, the light from the falling object gets redshifted as a consequence. So in fact it will take an infinite time for any object to fall into a black hole for an observer a long way off. In which case we would not get much gravitational radiation from the event ?
John Bannister
John,
Yes, the two explanations are a little contradictory. The “two arm” explanation is wrong. But two arms do help. And it’s more intuitive.
Yes, there is a time component to the distortion due to the gravitational wave. (Indeed, there must be.) This is why I said we should treat the mirrors as “test particles” that are moved by their interaction with the wave. If you think of it this way, then the space and time distortion don’t need to be disentangled. All we need to know is that, in the reference frame of one mirror, the other mirror moves away from it, meaning light will take longer to pass between the two mirrors.
Regarding your question of how gravitational waves escape the black holes: this is a question I get a lot. The misconception is that the gravitational waves come from INSIDE the black holes (or from exactly at the event horizon). Neither picture is quite true. Rather the gravitational waves come from the ambient spacetime, which the black holes are distorting.
Think about a boat. The boat creates a wake. But of course, the waves aren’t coming from INSIDE the boat. Rather they are coming from the distortion in the water as the boat moves through it.
Does this help?